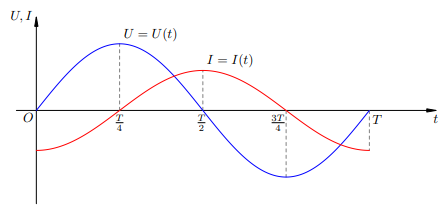
Мощность тока через катушку

Пусть на катушку подано переменное напряжение �=�0�����U=U0​sinωt. Ток через катушку отстаёт по фазе от напряжения на π/2:

�=�0sin⁡(��−�2)=−�0cos⁡��I=I0​sin(wt−2π​)=−I0​coswt

Для мгновенной мощности получаем:

�=��=−�0�0cos⁡��sin⁡��=−12�0�0sin⁡2��=−�0sin⁡2��P=UI=−U0​I0​coswtsinwt=−21​U0​I0​sin2wt=−P0​sin2wt

Снова средняя мощность оказывается равной нулю. Причины этого, в общем-то, те же, что и в случае с конденсатором. Рассмотрим графики напряжения и силы тока через катушку за период (рис. 1).

Рис.1. Напряжение на катушке и сила тока через неё

Мы видим, что в течение второй и четвёртой четвертей периода энергия поступает в катушку из внешней цепи. В самом деле, напряжение и сила тока имеют одинаковые знаки, сила тока возрастает по модулю; для создания тока внешнее электрическое поле совершает работу против вихревого электрического поля, и эта работа идёт на увеличение энергии магнитного поля катушки.

В первой и третьей четвертях периода напряжение и сила тока имеют разные знаки: катушка возвращает энергию в цепь. Вихревое электрическое поле, поддерживающее убывающий ток, двигает заряды против внешнего электрического поля и совершает тем самым положительную работу. А за счёт чего совершается эта работа? За счёт энергии, накопленной ранее в катушке.

Таким образом, энергия, запасаемая в катушке за одну четверть периода, полностью возвращается в цепь в ходе следующей четверти. Поэтому средняя мощность, потребляемая катушкой, оказывается равной нулю.

Мощность тока на произвольном участке

Теперь рассмотрим самый общий случай. Пусть имеется произвольный участок цепи — он может содержать резисторы, конденсаторы, катушки. . . На этот участок подано переменное напряжение �=�0�����U=U0​sinωt

Как мы знаем, между напряжением и силой тока на данном участке имеется некоторый сдвиг фаз α. Мы записывали это так:

�=�0sin⁡(��−�)I=I0​sin(wt−α)

Тогда для мгновенной мощности имеем:

�=�0�0sin⁡��sin⁡(��−�)P=U0​I0​sinwtsin(wt−a)

Теперь нам хотелось бы определить, чему равна средняя мощность. Для этого мы преобразуем выражение (1), используя формулу произведения синуса и косинуса:

�=12�0�0(cos⁡�−cos⁡(2��−�))(2)P=21​U0​I0​(cosα−cos(2wt−a))(2)

Но среднее значение величины cos(2ωt − α) равно нулю! Поэтому средняя мощность оказывается равной:

�‾=12�0�0cos⁡�(3)‾P=21​U0​I0​cosα(3)

Данную формулу можно записать с помощью действующих значений напряжения и силы тока:

�‾=�‾�‾����.P=UIcosα.

Формула (3) охватывает все три рассмотренные ситуации. В случае резистора имеем α = 0. Для конденсатора и катушки α = π/2, и средняя мощность равна нулю.

Кроме того, формула (3) даёт представление о весьма общей проблеме, связанной с передачей электроэнергии. Чрезвычайно важно, чтобы cos α у потребителя был как можно ближе к единице. Иначе потребитель начнёт возвращать значительную часть энергии назад в сеть (что ему совсем невыгодно), и к тому же возвращаемая энергия будет безвозвратно расходоваться на нагревание проводов и других элементов цепи.