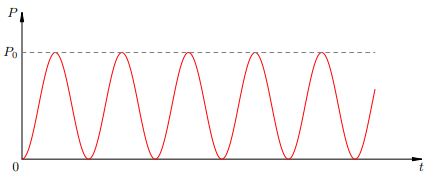
Мощность тока через резистор

Пусть переменный ток �=�0�����I=I0​sinωt протекает через резистор сопротивлением R. Напряжение на резисторе, как нам известно, колеблется в фазе с током:

�=��=�0������=�0�����U=IR=I0​Rsinωt=U0​sinωt

Поэтому для мгновенной мощности получаем:

�=��=�0�0���2��,P=UI=U0​I0​sin2ωt,

или

�=�0sin⁡2��(1)P=P0​sin2wt(1)

График зависимости мощности (1) от времени представлен на рис. 2. Мы видим, что мощность всё время неотрицательна — резистор забирает энергию из цепи, но не возвращает её обратно в цепь.

Рис. 1. Мощность переменного тока через резистор

Максимальное значение P0 нашей мощности связано с амплитудами тока и напряжения привычными формулами:

�0=�0�0=�02�=�02�P0​=U0​I0​=I02​R=RU02​​

На практике, однако, интерес представляет не максимальная, а средняя мощность тока. Это и понятно. Возьмите, например, обычную лампочку, которая горит у вас дома. По ней течёт ток частотой 50 Гц, т. е. за секунду совершается 50 колебаний силы тока и напряжения. Ясно, что за достаточно продолжительное время на лампочке выделяется некоторая средняя мощность, значение которой находится где-то между 0 и P0. Где же именно?

Посмотрите ещё раз внимательно на рис. 1. Cредняя мощность соответствует «середине» нашей синусоиды и принимает поэтому значение P0/2.

Разумеется, можно дать математически строгое определение среднего значения функции (в виде некоторого интеграла) и подтвердить нашу догадку прямым вычислением, но нам это не нужно. Достаточно интуитивного понимания простого и важного факта:

Cреднее значение квадрата синуса (или косинуса) за период равно 1/2.

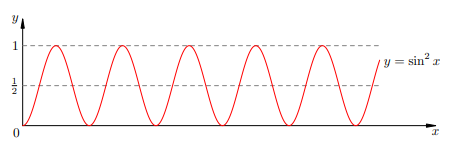
Этот факт иллюстрируется рисунком 2.

Рис. 2. Среднее значение квадрата синуса равно 1/2

Итак, для среднего значения <P> мощности тока на резисторе имеем:

�‾=�02=�0�02=�022�(2)P=2P0​​=2U0​I0​​=2RU02​​(2)

В связи с этими формулами вводятся так называемые действующие (или эффективные) значения напряжения и силы тока:

�‾=�02�‾=�02(3)U=2​U0​​I=2​I0​​(3)

Формулы (2), записанные через действующие значения, полностью аналогичны соответствующим формулам для постоянного тока:

�‾=�‾⋅�‾=�‾2�=�‾2�P=U⋅I=I2R=RU2​

Поэтому если вы возьмёте лампочку, подключите её сначала к источнику постоянного напряжения U, а затем к источнику переменного напряжения с таким же действующим значением U, то в обоих случаях лампочка будет гореть одинаково ярко.

Действующие значения (3) чрезвычайно важны для практики. Оказывается, вольтметры и амперметры переменного тока показывают именно действующие значения (так уж они устроены). Знайте также, что пресловутые 220 вольт из розетки — это действующее значение напряжения бытовой электросети.