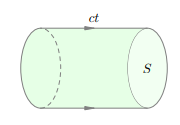
Плотность потока излучения

Электромагнитные волны переносят энергию из одних участков пространства в другие. Перенос энергии осуществляется вдоль лучей — воображаемых линий, указывающих направление распространения волны.

Важнейшей энергетической характеристикой электромагнитных волн служит плотность потока излучения.

Представим себе площадку площадью S, расположенную перпендикулярно лучам. Допустим, что за время t волна переносит через эту площадку энергию W. Тогда плотность потока излучения I определяетcя формулой:

�=���(1)I=StW​(1)

Иначе говоря, плотность потока излучения — это энергия, переносимая через единичную площадку (перпендикулярную лучам) в единицу времени; или, что то же самое — это мощность излучения, переносимая через единичную площадку. Единицей измерения плотности потока излучения служит Вт/м2Вт/м2.

Плотность потока излучения связана простым соотношением с плотностью энергии электромагнитного поля.

Фиксируем площадку S, перпендикулярную лучам, и небольшой промежуток времени t. Сквозь площадку пройдёт энергия:

�=���.(2)W=ISt.(2)

Эта энергия будет сосредоточена внутри цилиндра с площадью основания S и высотой ct (рис. 1), где c — скорость электромагнитной волны.

Рис. 1. К выводу формулы I = wc.

Объём данного цилиндра равен: V = Sct. Поэтому если w — плотность энергии электромагнитного поля, то для энергии W получим также:

�=��=����(3)W=wV=wSct(3)

Приравнивая правые части формул (2) и (3) и сокращая на St, получим соотношение:

�=��.(4)I=wc.(4)

Плотность потока излучения характеризует, в частности, степень воздействия электромагнитного излучения на его приёмники; когда говорят об интенсивности электромагнитных волн, имеют в виду именно плотность потока излучения.

Интересным является вопрос о том, как интенсивность излучения зависит от его частоты.

Пусть электромагнитная волна излучается зарядом, совершающим гармонические колебания вдоль оси X по закону x = x0 sin ωt. Циклическая частота ω колебаний заряда будет в то же время циклической частотой излучаемой электромагнитной волны.

Для скорости и ускорения заряда имеем: v = ˙x = x0ω cos ωt�=�˙=�0�cos⁡��v=x˙=x0​ωcosωt и �=�˙=−�0�2sin⁡��a=v˙=−x0​ω2sinωt. Как видим,�∼�2a∼ω2. Напряжённость электрического поля и индукция магнитного поля в электромагнитной волне пропорциональны ускорению заряда: E ∼ a и B ∼ a. Стало быть, �∼�2E∼ω2 и �∼�2B∼ω2.

Плотность энергии электромагнитного поля есть сумма плотности энергии электрического поля и плотности энергии магнитного поля:�=�эл+�магнw=wэл​+wмагн​. Плотность энергии электрического поля, как мы знаем, пропорциональна квадрату напряжённости поля: �эл∼�2wэл​∼E2. Аналогично можно показать, что �магн∼�2wмагн​∼B2. Следовательно, �эл∼�4wэл​∼ω4 и �магн∼�4wмагн​∼ω4, так что �∼�4w∼ω4.

Согласно формуле (1) плотность потока излучения пропорциональна плотности энергии: I ∼ w. Поэтому �∼�4I∼ω4. Мы получили важный результат: интенсивность электромагнитного излучения пропорциональна четвёртой степени его частоты.

Другой важный результат заключается в том, что интенсивность излучения убывает с увеличением расстояния до источника. Это понятно: ведь источник излучает в разных направлениях, и по мере удаления от источника излучённая энергия распределяется по всё большей и большей площади.

Количественную зависимость плотности потока излучения от расстояния до источника легко получить для так называемого точечного источника излучения.

Точечный источник излучения — это источник, размерами которого в условиях данной ситуации можно пренебречь. Кроме того, считается, что точечный источник одинаково излучает во всех направлениях.

Конечно, точечный источник является идеализацией, но в некоторых задачах эта идеализация отлично работает. Например, при исследовании излучения звёзд их вполне можно считать точечными источниками — ведь расстояния до звёзд настолько громадны, что их собственные размеры можно не принимать во внимание.

На расстоянии r от источника излучённая энергия равномерно распределяется по поверхности сферы радиуса r. Площадь сферы, напомним, S = 4πr2. Если мощность излучения нашего источника равна P, то за время t через поверхность сферы проходит энергия W = P t. С помощью формулы (1) получаем тогда:

�=��4��2�=�4��2I=4πr2tPt​=4πr2P​

Таким образом, интенсивность излучения точечного источника обратно пропорциональна расстоянию до него.