Импульс тела — это векторная величина, равная произведению массы тела на его скорость.

�⃗=��⃗p​=mv

Второй закон Ньютона в импульсной форме

Пусть �⃗F — равнодействующая сил, приложенных к телу массы m. Начинаем с обычной записи второго закона Ньютона:

��⃗=�⃗ma=F

С учётом того, что ускорение тела �⃗a равно производной вектора скорости, второй закон Ньютона переписывается следующим образом:

�����=�⃗mdtdv​=F

Вносим константу m под знак производной:

�(��⃗)��=�.⃗dtd(mv)​=F.

Как видим, в левой части получилась производная импульса:

��⃗��=�⃗dtdp​​=F

Второй закон Ньютона в импульсной форме.

Производная импульса тела есть равнодействующая приложенных к телу сил.

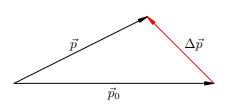
Можно сказать и так: результирующая сила, действующая на тело, равна скорости изменения импульса тела.

Производную в формуле можно заменить на отношение конечных приращений:

Δ�⃗Δ�=�⃗ΔtΔp​​=F

В этом случае �⃗F есть средняя сила, действующая на тело в течение интервала времени ∆t. Чем меньше величина ∆t, тем ближе отношение Δ�⃗Δ�ΔtΔp​​ к производной ��⃗��dtdp​​, и тем ближе средняя сила �⃗F к своему мгновенному значению в данный момент времени. В задачах, как правило, интервал времени ∆t достаточно мал.

Вектор Δ�⃗Δp​ в левой части соотношения называется изменением импульса за время ∆t.

Изменение импульса — это разность конечного и начального векторов импульса.

А именно, если �0⃗p0​​ — импульс тела в некоторый начальный момент времени, �⃗p​​— импульс тела спустя промежуток времени ∆t, то изменение импульса есть разность:

Δ�⃗=�⃗−�0⃗Δp​=p​−p0​​

Подчеркнём ещё раз, что изменение импульса — это разность векторов (рис. 1.). Напомним, что при построении разности векторов нужно совместить начала обоих векторов, соединить их концы и «уколоть» стрелкой тот вектор, из которого производится вычитание

Рисунок 1. Изменение импульса

Перепишем формулу 6 следующим образом:

Δ�⃗=�⃗Δ�Δp​=FΔt

Величина �⃗Δ�FΔtназывается импульсом силы. Словесная формулировка равенства такова:

Изменение импульса тела равно импульсу действующей на тело силы за данный промежуток времени.