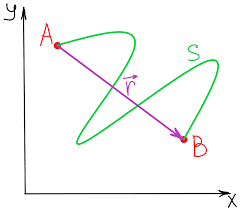
Траектория материальной точки — линия, описываемая в пространстве этой точки при ее движении.

В зависимости от формы траектории различают прямолинейное движение, движение по окружности, криволинейное движение и т.д.

Вектор — величина, характеризующаяся численным значением и направлением и, кроме того, векторы складываются по правилу параллелограмма.

Радиус-вектор r точки — вектор, проведенный из начала координат в данную точку.

Пусть материальная точка (в дальнейшем для краткости – частица) переместилась вдоль некоторой траектории из точки А в точку В(Рис.1).

Путь, пройденный частицей — расстояние между точками А и В, отсчитанное вдоль траектории.

Перемещение частицы — прямолинейный отрезок, проведенный из точки А в точку В.

Перемещения характеризуются численным значением и направлением и, кроме того, складываются по правилу параллелограмма.

Отсюда следует, что перемещение есть вектор.

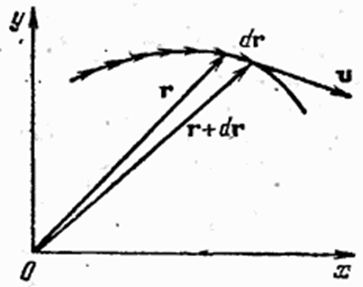
Рис. 1

В обычной жизни под скоростью понимают путь, проходимый частицей за единицу времени.

В физике под скоростью понимают следующее:

Скорость — векторная величина, характеризующая не только быстроту перемещения частицы по траектории, но и направление, в котором движется частица в каждый момент времени.

Зафиксировав некоторый момент времени t, рассмотрим приращение радиуса-вектора Δr за малый промежуток времени Δt следующий за t (Pис 2). Отношение Δr/Δt дает среднее значение скорости за время Δt. Если брать все меньшие промежутки Δt отношение Δ�/Δ�Δr/Δt в пределе даст значение скорости v в момент времени t.

�=lim⁡Δ�→0Δ�Δ�=����v=Δt→0lim​ΔtΔr​=dtdr​

Скорость — производная радиуса-вектора частицы по времени.

Перемещение dr совпадает с бесконечно малым элементом траектории. Следовательно, вектор скорости v направлен по касательной к траектории.

Рис. 2

Модуль скорости равен производной пути по времени.