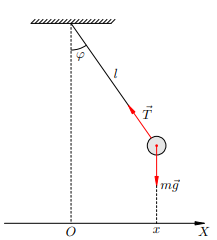
Математический маятник

Математический маятник — это небольшое тело, подвешенное на невесомой нерастяжимой нити.

(Рис. 1). Математический маятник может совершать колебания в вертикальной плоскости в поле силы тяжести.

Рисунок 1. Математический маятник

Найдём период малых колебаний математического маятника. Длина нити равна l. Сопротивлением воздуха пренебрегаем.

Запишем для маятника второй закон Ньютона:

��⃗=��⃗+�⃗ma=mg​+T

и спроектируем его на ось X:

���=��max​=Tx​

Если маятник занимает положение как на рисунке (т. е. x > 0), то:

��=−�����=−���Tx​=−Tsinφ=−lTx​

Если же маятник находится по другую сторону от положения равновесия (т. е. x < 0), то:

��=�����=−���Tx​=Tsinφ=−lTx​

Итак, при любом положении маятника имеем:

���=−���max​=−Tlx​

Когда маятник покоится в положении равновесия, выполнено равенство T = mg. При малых колебаниях, когда отклонения маятника от положения равновесия малы (по сравнению с длиной нити), выполнено приближённое равенство T ≈ mg. Воспользуемся им в формуле.

���=−����max​=−mglx​

или

��=−���ax​=−lg​x

Это — уравнение гармонических колебаний вида ��−�2�ax​−ω2x, в котором

�2=��w2=lg​

Следовательно, циклическая частота колебаний математического маятника равна:

�=��ω=lg​​

Отсюда период колебаний математического маятника:

�=2���T=2πgl​​

Обратите внимание, что в формулу не входит масса груза. В отличие от пружинного маятника, период колебаний математического маятника не зависит от его массы.