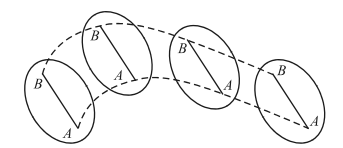
Поступательное движение

Поступательное движение — движение твердого тела, при котором прямая, соединяющая две любые точки тела, остается параллельной своему начальному направлению (рис. 1).

Рис. 1. Поступательное движение

При поступательном движении все точки тела описывают одинаковые (при наложении совпадающие) траектории и имеют в каждый момент времени одинаковые по модулю и направлению скорости и ускорения. Поэтому изучение поступательного движения твердого тела фактически сводится к задаче кинематики любого элемента тела (точки) и большой сложности не представляет.

Исследуя поведение тела, движущегося поступательно, можно считать, что масса тела сосредоточена в одной точке. К этой точке можно прикладывать все силы, действующие на тело. Размеры и форма тела на его движение не влияют.

Вращательное движение

Вращательное движение твердого тела вокруг неподвижной оси — движение твердого тела, при котором какие-либо две его точки остаются все время неподвижными.Прямая, проходящая через эти точки, называется осью вращения;

Все точки тела при вращательном движении описывают окружности в плоскостях, перпендикулярных к оси вращения и с центрами, лежащими на этой оси.

Любой радиус, проведенный от оси вращения до произвольной точки, за определенный промежуток времени повернется на один и тот же угол. Следовательно, угол поворота произвольного радиуса является характеристикой вращающегося твердого тела, аналогичной длине пути тела, движущегося поступательно. Если за определенный промежуток времени угол поворота ϕ для всех точек одинаковый, то и угловая скорость для всех точек тоже одинаковая. Связь между линейной v и угловой ω скоростью произвольной точки вращающегося тела, которая движется по окружности радиусом r, задается формулой:

�=��v=wr

Если угловая скорость ω изменяется, то:

Δ�=Δ(��)(1)Δv=Δ(wr)(1)

Разделим обе части равенства (1) на достаточно малый промежуток времени Δt :

Δ�Δ�=Δ(��)Δ�,Δ�Δ�=�Δ�Δ�(2)ΔtΔv​=ΔtΔ(wr)​,ΔtΔv​=rΔtΔw​(2)

В равенствах (2) слева — тангенциальное ускорение точки, движущейся по окружности радиусом R, т. е. ��=Δ�Δ�aτ​=ΔtΔv​. Справа величина Δ�Δ�ΔtΔw​ представляет собой угловое ускорение тела:

�=Δ�Δ�β=ΔtΔw​

Угловое ускорение β по модулю равно производной угловой скорости ω по времени t, т. е. �=����β=dtdw​

Напомним, что угловая скорость ω представляет собой псевдовектор, лежащий вдоль оси вращения, причем ориентация его связана с направлением вращения правилом правого винта, а модуль угловой скорости равен углу поворота тела за единицу времени. Таким образом, в случае неподвижной оси вектор углового ускорения направлен так же, как и вектор угловой скорости ω, если скорость вращения возрастает, и направлен в противоположную сторону, если скорость вращения убывает.

Основные кинематические характеристики вращательного движения тела — его угловая скорость ω и угловое ускорение β. Для любой точки тела, отстоящей от оси на расстоянии r, ее линейная скорость v r = ω, касательное (тангенциальное) ускорение ��=��aτ​=rβ нормальное ускорение ��=��2an​=rw2 и полное ускорение �=��2+�4a=rβ2+w4​

Связь между линейным и угловым ускорением дается формулой (2) или:

�=��a=rβ

Учитывая (2) и то, что Δω = ω − ω0 :

�=�0+��w=w0​+βt

что аналогично выражению для линейной скорости.

Если угол поворота радиуса выражать в радианах, то для произвольной точки длина дуги при повороте радиуса на угол ϕ будет равна �=��l=φr. Но l представляет собой длину пути, которую при равноускоренном движении можно представить следующим образом:

�=�0�+��22l=v0​t+2at2​

Подставляя значения: �=��,�0=�0�,�=��l=φr,v0​=w0​r,a=βr и сокращая на r, получаем:

�=�0�+��22(3)φ=w0​t+2βt2​(3)

Выражение (3) определяет угол поворота радиуса произвольной точки, иначе говоря, угол поворота вращающегося тела.

Плоское движение — комбинация поступательного и вращательного движений.