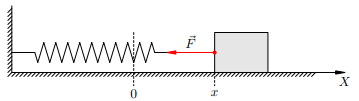
Пружинный маятник

Пружинный маятник — это закреплённый на пружине груз, способный совершать колебания в горизонтальном или вертикальном направлении.

Найдём период малых горизонтальных колебаний горизонтальном или вертикальном направлении. Найдём период малых горизонтальных колебаний пружинного маятника (рис. 1). Колебания будут малыми, если величина деформации пружины много меньше её размеров. При малых деформациях мы можем пользоваться законом Гука. Это приведёт к тому, что колебания окажутся гармоническими. Трением пренебрегаем. Груз имеет массу m, жёсткость пружины равна k. Координате x = 0 отвечает положение равновесия, в котором пружина не деформирована. Следовательно, величина деформации пружины равна модулю координаты груза.

Рисунок 1. Пружинный маятник

В горизонтальном направлении на груз действует только сила упругости F~ со стороны пружины. Второй закон Ньютона для груза в проекции на ось X имеет вид:

���=��max​=Fx​

Если x > 0 (груз смещён вправо, как на рисунке), то сила упругости направлена в противоположную сторону, и Fx < 0. Наоборот, если x < 0, то Fx > 0. Знаки x и Fx всё время противоположны, поэтому закон Гука можно записать так:

��==��Fx​==kx

Тогда соотношение принимает вид

���=−��max​=−kx

или

��=−���ax​=−mk​x

Мы получили уравнение гармонических колебаний, в котором

�2=��w2=mk​

Циклическая частота колебаний пружинного маятника, таким образом, равна:

�=��w=mk​​

Отсюда и из соотношения T = 2π/ω находим период горизонтальных колебаний пружинного маятника:

�=2���T=2πkm​​

Если подвесить груз на пружине, то получится пружинный маятник, совершающий колебания в вертикальном направлении. Можно показать, что и в этом случае для периода колебаний справедлива формула �=2���T=2πkm​​