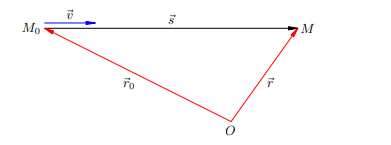
Равномерное прямолинейное движение материальной точки — это движение с постоянной скоростью �⃗υ.

Речь идёт о постоянстве вектора скорости; это значит, что скорость неизменна как по модулю, так и по направлению. Траекторией тела при равномерном прямолинейном движении служит прямая (или часть прямой — например, отрезок или луч). Вдоль данной прямой тело движется равномерно, то есть с постоянной по модулю скоростью.

Закон движения

Предположим, что тело, двигаясь равномерно и прямолинейно со скоростью �⃗v, переместилось за время t из точки �0M0​ в точку M (рис. 1).

Равномерное прямолинейное движение

Путь, пройденный телом, равен длине s вектора перемещения. Очевидно, что выполнено соотношение:

�=��s=vt

где v — модуль вектора скорости. Формула справедлива для произвольного равномерного движения (не обязательно прямолинейного). Но в случае прямолинейного равномерного движения эта формула становится соотношением между векторами. В самом деле, поскольку векторы �⃗s и�⃗v сонаправлены, формула позволяет записать:

�⃗=�⃗�s=vt

Как обычно, движение тела рассматривается в некоторой системе отсчёта, связанной с телом отсчёта O (рис. 1); Пусть �⃗0r0​ — радиус-вектор начальной точки �0M0​ и �⃗r — радиус-вектор конечной точки M. Тогда, очевидно,

�⃗=�⃗−�⃗0s=r−r0​

Подставим эту разность в формулу 1:

�⃗−�⃗0=�⃗�r−r0​=vt

Отсюда получаем закон движения (то есть зависимость радиус-вектора тела от времени):

�⃗=�⃗0+�⃗�r=r0​+vt

Переход от векторного соотношения к координатам осуществляется элементарно. Координаты точки �0M0​ обозначим (�0,�0,�0x0​,y0​,z0​). Они же являются координатами вектора �⃗0r0​. Координаты точки M (и вектора �⃗r) обозначим (x, y, z). Тогда векторная формула приводит к трём координатным соотношениям:

�⃗=�0+�⃗�x=x0​+vt

�⃗=�0+�⃗�y​=y0​+vt

�⃗=�0+�⃗�z=z0​+vt