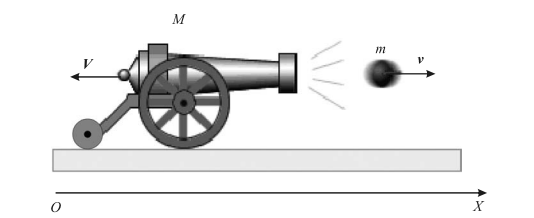
Реактивное движение; движение тела с переменной массой

Применим закон сохранения импульса к горизонтальному выстрелу из пушки. При стрельбе возникает отдача — ядро движется вперед, а пушка откатывается назад. Пусть пушка и ядро — два взаимодействующих тела, составляющих замкнутую систему. Скорость, которую приобретает пушка при отдаче, зависит от скорости ядра и соотношения масс пушки и ядра (рис. 1).

Принцип реактивного движения можно сформулировать так: если замкнутая система выбрасывает часть своей массы в каком-нибудь определенном направлении, то она приобретает импульс (количество движения) в противоположном направлении.

Рис. 1. Отдача при выстреле из пушки

Принцип реактивного движения позволил создать ракету — летательный аппарат, движущийся под действием реактивной силы, возникающей при отбросе массы сгорающего ракетного топлива (рабочего тела). Бывают неуправляемые и управляемые, изменяющие параметры траектории в полете; одно- и многоступенчатые (каждая ступень обеспечивает разгон ракеты на определенном участке, а затем отделяется) ракеты. Применяются в военном деле, космонавтике и др.

Движение тел может сопровождаться непрерывным изменением их массы. Например, масса движущейся капли может уменьшаться вследствие испарения или, наоборот, увеличиваться при конденсации паров на ее поверхности; масса ракеты при реактивном движении изменяется по мере сгорания топлива и т. д. Изменение массы тел приводит к некоторому усложнению формул, по которым рассчитывается их движение.

Выведем уравнение движения тел с уменьшающейся массой при некоторых упрощающих предположениях. Допустим, что в начальный момент времени тело с массой �0M0​ покоилось относительно некоторой системы отсчета, связанной, например, с Землей. По истечении времени t масса тела сделалась равной M, а скорость — v. За каждый промежуток времени от тела отделяется масса dm, причем будем предполагать, что по окончании процесса отделения каждая из этих элементарных масс имеет одну и ту же конечную скорость u. Далее предположим, что на тело не действуют внешние силы, поэтому выбрасывание массы dm производится силами взаимодействия �1f1​ и �2f2​ между телом и его отделяющимися частями. Эти внутренние силы по третьему закону Ньютона равны по величине и противоположны по направлению. За время dt масса тела уменьшается на dM, а скорость — увеличивается на dv. Сила �1f1​, действующая на массу M-dM, изменяет ее импульс на величину, равную:

�1��=(�−��)⋅(�+��)−(�−��)�≈���f1​dt=(M−dM)⋅(v+dv)−(M−dM)v≈Mdv

Сила, действующая на выбрасываемую массу dm, изменяет скорость ее движения от начального значения v до конечного u :

�2��=(�−�)��f2​dt=(u−v)dm

Так как �1=−�2f1​=−f2​, а отделяющаяся масса dm равняется уменьшению массы тела, т. е. dm=-dM, то импульс, приобретаемый телом за время dt, будет равен:

���=(�−�)��(1)Mdv=(u−v)dM(1)

Разность скоростей (u-v=w ) есть относительная скорость отделяющихся масс относительно самого тела (по абсолютной величине (w=u+v); для ракеты это есть средняя скорость выбрасываемых продуктов сгорания относительно корпуса ракеты. Так как w направлена противоположно скорости dv, то при замене векторного уравнения (1) скалярным, вместо (u-v) следует написать −w :

��=−����dv=−wMdM​

Знак «минус» означает, что увеличение скорости тела (положительное dv ) сопровождается уменьшением массы тела (отрицательное dM).

Если дополнительно предположить, что скорость w отделяющихся масс относительно самого тела сохраняется в процессе движения постоянной, то уравнение ��=−����dv=−wMdM​ легко интегрируется, и в результате получается формула Циолковского:

�=�ln⁡(1+�0−��)=�ln⁡(1+����)v=wln(1+MM0​−M​)=wln(1+MP​MT​​)

где Mт — начальная масса топлива; Mр — масса ракеты без топлива. Отношение ����MP​MT​​ называют числом Циолковского. Полученная Циолковским формула ����=exp⁡(��)−1MP​MT​​=exp(wv​)−1 позволяет рассчитывать запас топлива, необходимого для сообщения ракете скорости v.