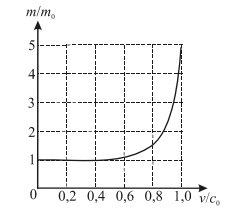
Релятивистская масса

В течение многих лет при решении задач механики использование законов Ньютона приводило к правильным результатам. Однако в начале XX в. при изучении движения очень быстрых электронов в электрических и магнитных полях оказалось, что результаты экспериментов не совпадают с расчетами, выполненными с применением второго закона Ньютона в его классической форме. Стало ясно, что классическая механика не универсальна и не пригодна для решения любых задач.

В соответствии с релятивистской механикой масса движущегося тела m зависит от скорости его движения v :

�=�01−�2�02=�0�m=1−c02​v2​​m0​​=m0​γ

где m — релятивистская масса; �0m0​ — масса покоя тела.

Релятивистский импульс

Релятивистская масса больше массы покоя �0m0​ и зависит от скорости v. Масса одной и той же частицы различна в разных инерциальных системах, движущихся относительно одной из них с различными скоростями. Масса покоя �0m0​ является характеристической величиной частицы.

Зависимость свойств пространства и времени от движения системы отсчета приводит к тому, что сохраняющейся при любых взаимодействиях тел является величина:

�=�0�1−�2�02(1)p=1−c02​v2​​m0​v​(1)

называемая релятивистским импульсом.

При �/�0≪1v/c0​≪1 выражение для импульса переходит в то, которое используется в механике Ньютона p = mv, где под m понимается масса покоя «классической» частицы ( �=�0m=m0​ ), ибо при �/�0≪1v/c0​≪1 различие между m и �0m0​ несущественно. Однако при скоростях, близких к скорости света (релятивистские скорости), только выражение (1) дает правильные результаты, согласующиеся с экспериментом.

Классический закон сложения скоростей и классический закон сохранения импульса являются частными случаями универсальных релятивистских законов и выполняются только при значениях скоростей, значительно меньших скорости света в вакууме.

Возрастание массы тела с увеличением скорости приводит к тому, что ни одно тело с массой покоя, не равной нулю, не может достигнуть скорости, равной скорости света в вакууме. Скорость v, большая �0c0​, теоретически приводит для обычных частиц к мнимой массе и мнимому импульсу, что физически бессмысленно. Зависимость массы от скорости начинает сказываться лишь при скоростях, близких к �0c0​ (рис. 1).

Рис. 1. Зависимость массы от скорости

Приведенные здесь формулы неприменимы к фотону, т. к. у него отсутствует масса покоя ( �0=0m0​=0). Фотон всегда движется со скоростью, равной скорости света в вакууме, и является ультрарелятивистской частицей. Тем не менее, отсюда не следует постоянство скорости света во всех веществах. Уравнение

����=�dtdp​=F

удовлетворяет требованиям теории относительности, если импульс релятивистской частицы описывается формулой (1). Следовательно, основное уравнение релятивистской динамики имеет вид

���(�0�1−�2�02)=�dtd​⎝⎛​1−c02​v2​​m0​v​⎠⎞​=F

Основное уравнение релятивистской динамики инвариантно по отношению к преобразованиям Лоренца. Сила F в релятивистской динамике не инвариантна: в разных инерциальных системах отсчета ее численное значение и направление различны.

Кинетическая энергия релятивистской частицы

Кинетическую энергию релятивистской частицы можно определить следующим образом:

��=�−�0EK​=E−E0​��=�02(�01−�2−�0)=�02(�−�0)=�02Δ�EK​=c02​(1−β2​m0​​−m0​)=c02​(m−m0​)=c02​Δm

где Е — полная энергия; �0E0​ — энергия покоя. В данном случае мы рассматриваем только кинетическую энергию, т. е. не учитываем возможность релятивистской частицы взаимодействовать с внешними полями.

Приращение кинетической энергии релятивистской частицы пропорционально приращению релятивистской массы частицы. Кинетическая энергия релятивистской частицы равна разности ее полной энергии и ее энергии покоя. При малых скоростях частиц выражение для кинетической энергии частицы принимает вид выражения, принятого в классической механике.