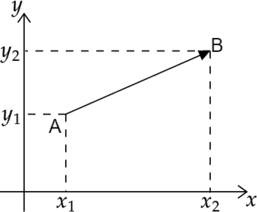
В физике рассматриваются как скалярные (время, масса, температура и т.д.), так и векторные величины (скорость, сила, импульс и др.).

Скалярными называются величины, определяемые численным значением и единицей измерения.

Векторными называются величины, характеризуемые численным значением, единицей измерения и направлением.

Векторные величины изображаются направленными отрезками (векторами). Численное значение вектора называется его модулем.

Длина вектора — расстояние между началом и концом вектора.

Длина векторов обозначается следующим образом: |�⃗a| или |��⃗AB|. Если задана прямоугольная система координат, и координаты начала и конца вектора заданы в ней парами �=(�1;�1)A=(x1​;y1​) и �=(�2;�2)B=(x2​;y2​) соответственно, тогда координаты вектора можно задать ��⃗={�2−�1,�2−�1}AB={x2​−x1​,y2​−y1​}

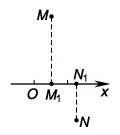
Тогда длина вектора ��⃗AB задается формулой:

∣��∣⃗=(�2−�1)2−(�2−�1)2∣AB∣​=(x2​−x1​)2−(y2​−y1​)2​

При решении задач часто используется понятие проекция вектора на ось. Начнем с понятия проекция точки на ось.

Проекция точки — это основание перпендикуляра, опущенного из данной точки на ось.

M1,N1 - проекции точек M,N на ось OX

Проекцией вектора на какую-либо ось называется длина отрезка между проекциями начала и конца вектора на эту ось, взятая со знаком «+» или «−».

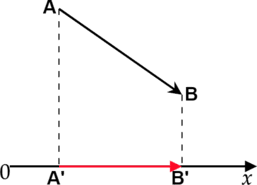
Проекция вектора AB на ось OX