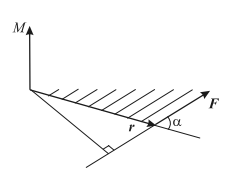
Вращательное движение абсолютно твердого тела вокруг неподвижной оси

Рассмотрение вращательного движения наряду с ранее уже введенными физическими параметрами (угол поворота, угловая скорость, угловое ускорение) требует введения совершенно новых, специфичных для вращательного движения, параметров.

Вращательное действие силы зависит не только от самой силы, но и от точки ее приложения, т. е. «плеча», и распределения массы относительно оси вращения.

Момент силы — величина, характеризующая вращательный эффект силы; имеет размерность произведения длины на силу.

Различают момент силы относительно центра (точки) и относительно оси.

Момент силы (вращающий момент) M относительно неподвижной оси определяется векторным произведением M= [ r, F], где F — вектор силы, лежащий в плоскости вращения, r — радиус-вектор в той же плоскости, направленный от оси вращения к точке приложения силы F (рис. 1). Вектор M параллелен оси вращения, направление его совпадает с направлением поступательного движения правого винта (буравчика) при его вращении от r к F. По модулю момент силы M = rFsin( r,F ).

Рис. 1. Взаимное расположение векторов

Момент силы относительно точки — векторная величина, равная векторному произведению радиус-вектора, проведенного из центра в точку приложения силы, на силу (рис. 2).

Рассмотрим движение материальной точки вокруг неподвижной оси с угловой скоростью ω. Пусть r — радиус-вектор материальной точки (от оси вращения), а m — ее масса. Тогда линейная скорость этой точки:

�=[��](1)v=[wr](1)

а момент импульса относительно оси вращения — псевдовектор L :

�=[���]L=[rmv]

Момент импульса (кинетический момент, момент количества движения, орбитальный момент, угловой момент) материальной точки относительно центра вращения — псевдовектор, равный векторному произведению радиус-вектора точки, проведенного из центра, на ее количество движения.

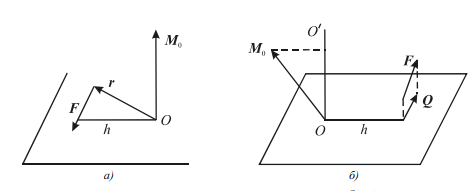
Рис. 2. Момент силы относительно центра O (а) и момент силы относительно оси OO′ (б)

Момент силы M относительно неподвижной оси вращения равен отношению изменения момента импульса относительно этой оси вращения ко времени, за которое произошло это изменение:

�=����M=dtdL​

Ранее мы отмечали, что сила действия одного тела на второе равна силе действия второго тела на первое, и эти силы направлены противоположно. Роль силы в случае вращения будет играть момент силы, роль скорости — угловая скорость, роль массы — момент инерции.