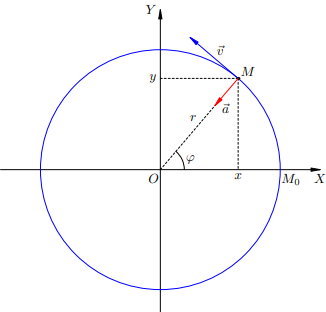
Закон движения

Найдём зависимость координат вращающейся точки от времени. Из рис. 1,

Рисунок 1.Равномерное движение по окружности

�=�����x=rcosφ�=�sin⁡�y=rsinφ

�=������x=rcosωt

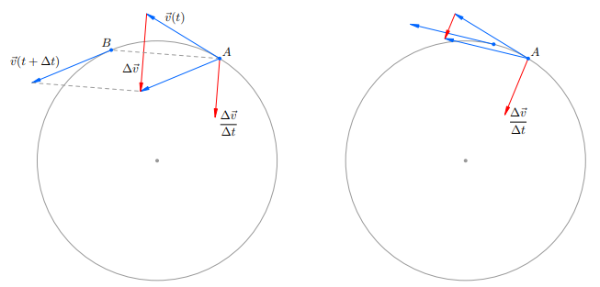
�=������.y=rsinωt.

Формулы являются решением основной задачи механики для равномерного движения точки по окружности.

Центростремительное ускорение

�=−�2�,a=−ω2r,

где �⃗r — радиус-вектор вращающейся точки.

Мы видим, что вектор ускорения направлен противоположно радиус-вектору, т. е. к центру окружности (см. рис. 1.). Поэтому:

Центростремительное ускорение — ускорение точки, равномерно движущейся по окружности.

Получаем выражение для модуля центростремительного ускорения:

�=�2�a=ω2r

Если вместо �ωподставим формулу ��rv​ и получим:

�=�2�a=rv2​

При любом КД возникает центростремительное ускорение, направленное к центру.

Рисунок 2. Центростремительное ускорение, направленное к центру