Консервативные силы называются так потому, что сохраняют механическую энергию замкнутой системы тел.

Механическая энергия E тела равна сумме его кинетической и потенциальной энергий:

�=�+�E=K+W

Механическая энергия системы тел равна сумме их кинетических энергий и потенциальной энергии их взаимодействия друг с другом. Предположим, что тело совершает движение под действием силы тяжести и/или силы упругости пружины. Будем считать, что трения нет. Пусть в начальном положении кинетическая и потенциальная энергии тела равны �1K1​ и �1W1​, в конечном положении — �2K2​ и �2W2​. Работу внешних сил при перемещении тела из начального положения в конечное обозначим A. По теореме о кинетической энергии:

�2−�1=�K2​−K1​=A

Но работа консервативных сил равна разности потенциальных энергий:

�=�1−�2A=W1​−W2​

Отсюда получаем:

�2−�1=�1−�2K2​−K1​=W1​−W2​

или

�1+�1=�2+�2K1​+W1​=K2​+W2​

Левая и правая части данного равенства представляют собой механическую энергию тела в начальном и конечном положении:

�1=�2E1​=E2​

Следовательно, при движении тела в поле силы тяжести и/или на пружине механическая энергия тела остаётся неизменной при отсутствии трения. Справедливо и более общее утверждение.

Закон сохранения механической энергии.

Если в замкнутой системе действуют только консервативные силы, то механическая энергия системы сохраняется.

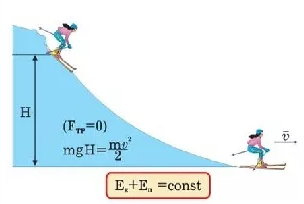
При этих условиях могут происходить лишь превращения энергии: из кинетической в потенциальную и наоборот. Общий запас механической энергии системы остаётся постоянным.

�к+�п=�����Eк​+Eп​=const

Закон сохранения механической энергии