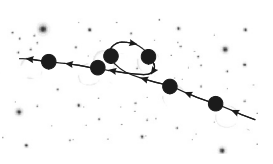
Законы Кеплера

Небесная механика — раздел астрономии, изучающий движения тел Солнечной системы в их общем гравитационном поле.

В ряде случаев (в теории движения комет, спутников и др.) кроме гравитационных сил учитываются реактивные силы, давление излучения, сопротивление среды, изменение массы и другие факторы.

С точки зрения земного наблюдателя планеты движутся по весьма сложным траекториям (рис. 1). Первая попытка создания модели Вселенной была предпринята Птолемеем (~ 140 г.). В центре мироздания Птолемей поместил Землю, вокруг которой по большим и малым кругам, как в хороводе, двигались планеты и звезды.

Рис. 1. Условное изображение наблюдаемого движения Марса на фоне неподвижных звезд

Датский астроном Тихо Брáге решил, что нужно внимательно следить за тем, где появляются на небе планеты и точно это записывать. Это было началом современной науки, ключом к правильному пониманию природы — наблюдать за предметом, записывать все подробности и надеяться, что полученные таким способом сведения послужат основой для того или иного теоретического истолкования. Браге, владевший островом поблизости от Копенгагена, оборудовал в 1576 г. этот остров большими бронзовыми кругами и наблюдательными пунктами (обсерватория «Ураниборг») и свыше 20 лет записывал положения планет.

Когда все эти данные были собраны, они попали в руки Кеплера, который и попытался решить, как движутся планеты вокруг Солнца. Он искал решение методом проб и ошибок. Однажды ему показалось, что он уже получил ответ: он решил, что планеты движутся по кругу, но Солнце лежит не в центре. Потом Кеплер заметил, что одна из планет (Марс) отклоняется от нужного положения на 8 угловых минут, и понял, что полученный им результат неверен, т. к. Браге не мог допустить такую большую ошибку. Уверенный в точности наблюдений, он решил пересмотреть свою теорию и, в конце концов, обнаружил три факта, позднее сформулированные как «законы Кеплера».

Сначала (15 мая 1618 г.) Кеплер установил, что планеты движутся вокруг Солнца по эллипсам, и Солнце находится в одном из фокусов.

Эллипс (овал) — это геометрическое место точек, сумма расстояний которых от двух заданных точек (фокусов) есть величина постоянная (рис. 2).

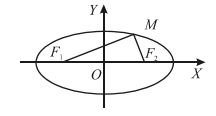
Рисунок 2. Эллипс

Первый закон Кеплера — планеты обращаются по эллипсам, в одном из фокусов которых находится Солнце (рис. 3).

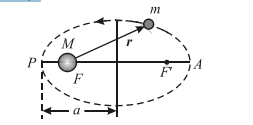
Рисунок 3. Эллиптическая орбита планеты массой m M. a — длина большой полуоси, F и F′ — фокусы орбиты

По мере движения планеты по эллиптической орбите ее расстояние от Солнца непрерывно изменяется. Ближайшую к Солнцу точку орбиты называют перигелием (P), а наиболее далекую — афелием (Α). Полусумма перигелийного q и афелийного Q расстояний выражает среднее расстояние планеты от Солнца, равное большой полуоси ее орбиты a :

�+�2=�(1)2Q+q​=a(1)

Земля проходит перигелий в начале января, а афелий — в начале июля. В связи с этим зима в северном полушарии короче и мягче, чем в южном, а лето продолжительнее и прохладнее.

Важной характеристикой орбиты является ее эксцентриситет e, определяемый соотношением:

�−�2�=�(2)2aQ−q​=e(2)

Все планеты Солнечной системы движутся по орбитам, близким к круговым (т. е. эксцентриситеты их орбит близки к 0).

Кеплер также обнаружил, что если взять два положения планеты, отделенных друг от друга определенным промежутком времени, потом взять другую часть орбиты и там — тоже два положения планеты, разделенных этим же промежутком времени, и провести линии (радиус-векторы) от Солнца к планете, то площадь, заключенная между орбитой планеты и парой линий, которые отделены друг от друга тремя неделями, одинакова в любой части орбиты (рис. 1). А чтобы эти площади были одинаковые, планета должна идти быстрее, когда она ближе к Солнцу, и медленнее, когда она далеко от него.

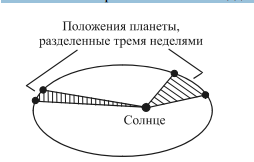
Рисунок 4. Ко второму закону Кеплера

Второй закон Кеплера — радиус-вектор планеты за равные промежутки времени описывает равновеликие площади (рис. 2).

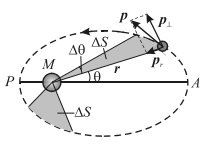
Рисунок 5. Закон площадей — 2-й закон Кеплера

Орбитальная скорость планеты изменяется в некоторых пределах: от наибольшей в перигелии до наименьшей в афелии.

Еще через несколько лет Кеплер сформулировал третье правило, которое касалось не движения одной планеты вокруг Солнца, а связывало движение различных планет друг с другом. Оно гласило, что время полного оборота планеты вокруг Солнца зависит от величины орбиты и пропорционально квадратному корню из куба этой величины. А величиной орбиты считается большая полуось эллипса.

Третий закон Кеплера — квадраты периодов обращения планет вокруг Солнца относятся между собой как кубы больших полуосей их орбит.

Третий закон Кеплера удобно выразить формулой, по которой можно вычислить относительные расстояния планет от Солнца:

�12�22=�13�23T22​T12​​=Q23​Q13​​

Законы Кеплера были объяснены и уточнены на основе закона всемирного тяготения Ньютона.