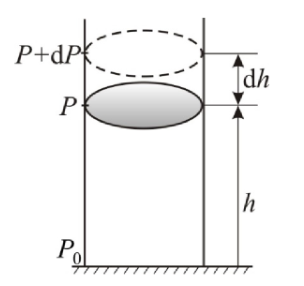
Барометрическая формула

Атмосферное давление на какой-либо высоте ℎh обусловлено весом слоёв газа, лежащих выше. Пусть �P – давление на высоте ℎh, а �+��P+dP - на высоте ℎ+�ℎh+dh.

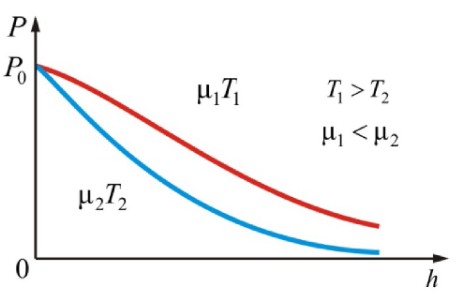
Давление P, P+dP на высотах h, h+dh соответственно

Разность давления �−(�+��)P−(P+dP) равна весу газа, заключённого в объёме цилиндра с площадью основания, равной единице, и высотой �ℎdh.

Так как �=��ℎP=ρgh, где �=��/��ρ=Pμ/RT — плотность газа на высоте ℎh, медленно убывающая с высотой, то можно записать: �−(�+��)=���ℎP−(P+dP)=ρgdh.

Отсюда можно получить барометрическую формулу, показывающую зависимость атмосферного давления от высоты:

�=�0exp⁡(−��ℎ��)P=P0​exp(−RTμgh​)

Из барометрической формулы следует, что давление убывает с высотой тем быстрее, чем тяжелее газ (чем больше и чем ниже температура. Например, на больших высотах концентрация легких газов НеНе и Н2Н2​ гораздо больше, чем у поверхности Земли.

Зависимость давления от высоты при разных молярных массах и температурах

Распределение Больцмана

Исходя из основного уравнения молекулярно-кинетической теории �=���P=nkT, заменим �P и �0P0​ в барометрической формуле на �n и �0n0​ и получим распределение молекул во внешнем потенциальном поле – распределение Больцмана:

�=�0exp⁡(−��ℎ��), или �=�0exp⁡(−��ℎ��)n=n0​exp(−RTμgh​), или n=n0​exp(−kTmgh​)

где �0n0 и �n – число молекул в единичном объёме на высоте ℎ=0h=0 и ℎh.

С уменьшением температуры число молекул на высотах, отличных от нуля, убывает. При Т=0Т=0 тепловое движение прекращается, все молекулы расположились бы на земной поверхности. При высоких температурах, наоборот, молекулы оказываются распределёнными по высоте почти равномерно, а плотность молекул медленно убывает с высотой. Так как mgh – это потенциальная энергия ЕпЕп​, то на разных высотах Еп=��ℎЕп​=mgh – различна. Следовательно, уравнение (3.2.5) характеризует распределение частиц по значениям потенциальной энергии:

�=�0exp⁡(−�п��)n=n0​exp(−kTEп​​)

Данное уравнение является законом распределения частиц по потенциальным энергиям — распределение Больцмана.

Закон Максвелла-Больцмана

Итак, закон Максвелла даёт распределение частиц по значениям кинетической энергии, а закон Больцмана – распределение частиц по значениям потенциальной энергии. Учитывая, что полная энергия �=Еп+ЕкE=Еп​+Ек​, оба распределения можно объединить в единый закон Максвелла-Больцмана:

��=�0�exp⁡(−�п��)dn=n0​Aexp(−kTEп​​)