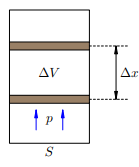
Работа газа в изобарном процессеПредположим, что газ расширяется при постоянном давлении p. Тогда сила F, с которой газ действует на поршень, также постоянна. Пусть поршень переместился на расстояние Δ�Δx(рис. 1). Работа газа равна: �=�Δ�=��Δ�A=FΔx=pSΔx
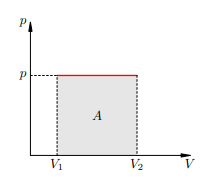
Рисунок 1. A = p∆V Но �Δ�=Δ�SΔx=ΔV — изменение объёма газа. Поэтому для работы газа при изобарном расширении мы получаем формулу: �=�Δ�A=pΔV Если V1 и V2 — начальный и конечный объём газа, то для работы газа имеем: �=�(�2−�1)A=p(V2−V1) Изобразив данный процесс на pV -диаграмме, мы видим, что работа газа равна площади прямоугольника под графиком нашего процесса(рис. 2).
Рисунок 2. Работа газа как площадь Пусть теперь газ изобарно сжимается от объёма V1 до объёма V2. С помощью аналогичных рассуждений приходим к формуле: �=−�(�1−�2).A=−p(V1−V2). Но −(�1−�2)=�2−�1=Δ�−(V1−V2)=V2−V1=ΔV , и снова получается формула. Работа газа опять-таки будет равна площади под графиком процесса на pV -диаграмме, но теперь со знаком минус. Итак, формула �=�Δ�A=pΔV выражает работу газа при постоянном давлении — как в процессе расширения газа, так и в процессе сжатия. | |
| Просмотров: 138 | |