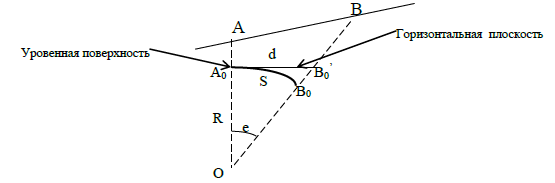
Пусть на земной поверхности измерена линия АВ. Замена проекции линии на уровенную поверхность �0�0A0​B0​ (s) горизонтальным проложением �0�0′A0​B0′​(d) повлечет за собой погрешность Δ�=�−�Δd=d−s.

Учет кривизны Земли

Из известных математических зависимостей можно записать, что

�=����;���=�+�33+⋯;�=��=��.d=Rtge;tge=e+3e3​+⋯;e=Rs​=Rd​.

Тогда,

Δ�=�(�+�33)−��33=�33�2;Δd=R(e+3e3​)−R3e3​=3R2d3​;Δ��=�23�3.dΔd​=3R3d2​.

В геодезической практике наивысшая точность измерения расстояний достигает

Δ��=1106dΔd​=1061​

Тогда

�2=3�2106=3⋅40⋅106106,d2=1063R2​=3⋅40⋅106106​,�=11км.d=11км.

Следовательно, участки земной поверхности радиусом 11 км можно считать плоскими и кривизной Земли пренебрегать.

При измерении превышений погрешность Δℎ(�0�0′)Δh(B0​B0′​), связанную с кривизной Земли, получим из следующих формул

�2+�2=(�+Δℎ)2,R2+d2=(R+Δh)2,�2=2�⋅Δℎ+Δℎ2,d2=2R⋅Δh+Δh2,Δℎ≈�22�Δh≈2Rd2​

Подставляя в последнюю формулу различные значения d, получим соответствующие значения ΔℎΔh:

Такие расхождения высоты между уровенной поверхностью и горизонтальной плоскостью учитываются при строительстве различных сооружений (например, тоннелей) и выполнении высокоточных геодезических измерений.