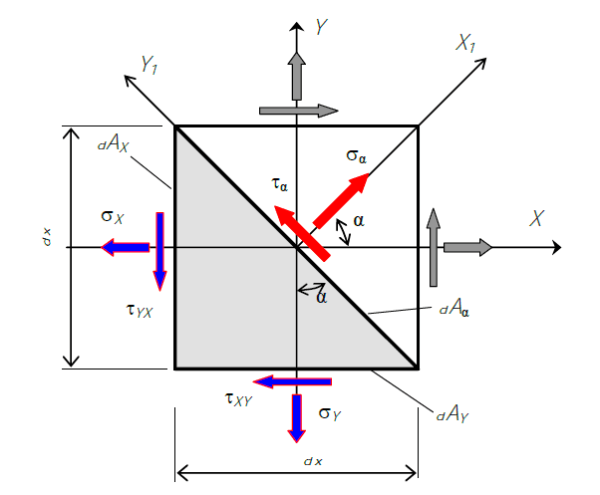
Если оси X_1 и Y_1 поворачивать, то при каком-то положении на наклонной площадке нормальное напряжение достигнет экстремального значения. Найдем положение такой площадки.

Напряжения, действующие на грани элемента и на наклонную площадку

�����=(�����2�+�����2�+������2�)′==−��2����⋅����+��2����⋅����+���2���2�dαdσα​​=(σx​cos2α+σy​sin2α+τxy​sin2α)′==−σx​2sinα⋅cosα+σy​2sinα⋅cosα+τxy​2cos2α

Далее уравнение разделим на 2 и приведем подобные:

−��−��2⋅���2�+���⋅���2�=0−2σx​−σy​​⋅sin2α+τxy​⋅cos2α=0

Слагаемые второго уравнения умножим на 2, разделим на cos2α и на (��−��σx​−σy​) получим формулу для определения угла наклона такой особенной площадки, на которой нормальное напряжение принимает экстремальное значение:

��(2�)=−2�����−��tg(2α)=−σx​−σy​2τxy​​​

Убеждаемся, что касательные напряжения на этих площадках равны нулю:

��=−��−��2���2�+������2�=0τα​=−2σx​−σy​​sin2α+τxy​cos2α=0

Эти площадки настолько важны в механике твердого деформированного тела, что им присвоено специальное название.

Три взаимно перпендикулярные площадки, на которых касательные напряжения равны нулю, а нормальные напряжения принимают экстремальные значения, называются главными площадками.

Нормальные напряжения, действующие на главных площадках, называются главными напряжениями.

Главные напряжения индексируются цифрами. Для удобства и сокращения записей принята индексация главных напряжений по условию:

�1⩾�2⩾�3σ1​⩾σ2​⩾σ3​

Главные напряжения для плоского напряженного состояния вычисляются по формуле (без вывода):

�1,3=��+��2±12(��−��)2+4���2σ1,3​=2σx​+σy​​±21​(σx​−σy​)2+4τxy2​​​

Недостающее главное напряжение равно нулю.