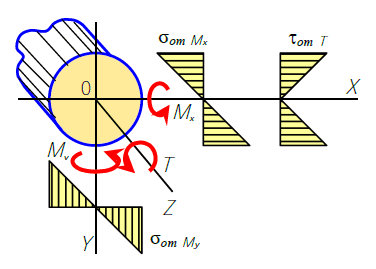
При изгибе с кручением в поперечных сечениях стержня появляются изгибающий и крутящий моменты. На кручение с изгибом работают элементы пространственных конструкций, валы машин, винтовые пружины и др.

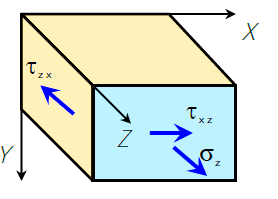
Распределение напряжений от внутренних сил при изгибе с кручением

Рассмотрим стержень круглого сечения. Учитывая принцип независимости действия сил, напряжения в произвольной точке сечения равны сумме напряжений от кручения и от изгиба:

�от��=�����;�от��=�����;�от�=����σотMx​=Ix​Mx​​y;σотMy​=Iy​My​​x;τотT​=Ip​T​p

Анализ эпюр показывает, что опасная точка, обозначим ее буквой S, располагается на контуре сечения. Выделим около точки S элементарный параллелепипед.

Элемент, вырезанный вблизи поверхности стержня круглого сечения

Для установления связи между моментами и координатами точки S, используются элементы векторной алгебры. Окончательно, для третьей теории прочности:

����=��пр��≤�σIII=Wx​Muпр​​≤R​

Где:

��пр=��2+�2Muпр​=Mu2​+T2​

По четвертой теории прочности имеем:

����=��пр��≤�σIII=Wx​Muпр​​≤R​

Где:

��пр=��2+0,75⋅�2Muпр​=Mu2​+0,75⋅T2​