При поперечном изгибе в поперечных сечениях балки кроме изгибающих моментов появляются еще и поперечные силы, а, следовательно, и касательные напряжения. Согласно закону парности касательных напряжений и в продольных сечениях балки будут появляться касательные напряжения. Эти напряжения вызывают сдвиг продольных слоев (волокон) относительно друг друга, что приводит к искривлению поперечных сечений.

Искривление поперечных сечений называется депланацией сечений.

Экспериментально установлено, что величина депланации сечения зависит от отношения длины балки к высоте ее сечения.

Депланация поперечных сечений за счет касательных напряжений

Различают балки по отношению ее длины к высоте поперечного сечения:

Установлено, что депланация поперечных сечений в тонких балках незначительная и ею можно пренебречь. Поэтому формула для нормальных напряжений в тонких балках при поперечном изгибе вполне приемлема.

�=�����σ=Ix​Mx​​y

Расчет толстых балок (плит) выполняется методами теории упругости и в сопротивлении материалов не рассматривается.

Рассмотрим балку, испытывающую поперечный изгиб.

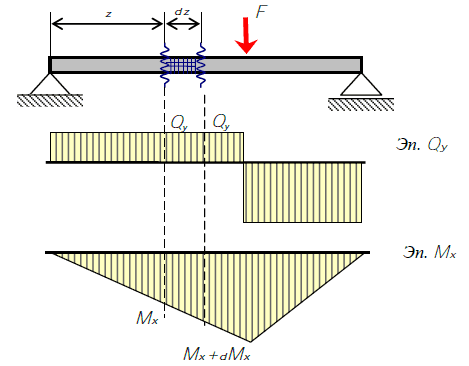
Балка, испытывающая поперечный изгиб

Двумя сечениями выделим элементарный участок на балке и рассмотрим его подробнее.

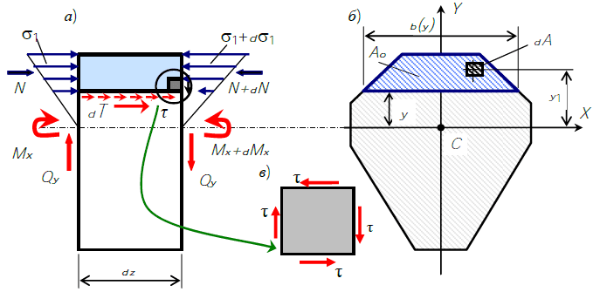
Элемент балка, подвергнутый действию нормальных и касательных напряжений в поперечных и продольных сечениях при поперечном изгибе

В левом сечении изгибающий момент равен ��Mx​, а в правом ��+���Mx​+dMx​. Поэтому нормальные напряжения в отмеченной точке отличаются и равны слева:

�1=�����1σ1​=Ix​Mx​​y1​

а справа

�1+��1=��+������1σ1​+dσ1​=Ix​Mx​+dMx​​y1​

Отсюда следует, что изменение нормального напряжения на расстоянии dz равно:

��1=�1+��1−�1=��+������1−�����1=������1dσ1​=σ1​+dσ1​−σ1​=Ix​Mx​+dMx​​y1​−Ix​Mx​​y1​=Ix​dMx​​y1​

Тогда приращение силы равно:

��=∫�0��1��=∫�0������1��=�����∫�0�1��=�������0dN=∫A0​​dσ1​dA=∫A0​​Ix​dMx​​y1​dA=Ix​dMx​​∫A0​​y1​dA=Ix​dMx​​Sx0​

Допущение — будем полагать, что касательные напряжения распределяются по ширине сечения равномерно.

Поэтому равнодействующую касательных напряжений в горизонтальном сечении можно вычислить по формуле:

��=�⋅��⋅�dT=τ⋅dz⋅b

Из условия равновесия справедливо равенство:

��=��dT=dN

Подставим выражения для dT и dN и получим:

��=�⋅��⋅�=��=�������0dT=τ⋅dz⋅b=dN=Ix​dMx​​Sx0​

Отсюда следует выражение для касательного напряжения в продольном сечении балки на выделенном участке:

�=�����⋅��0���=����0���τ=dzdMx​​⋅Ix​bSx0​​=Ix​bQy​Sx0​​

Учитывая закон парности касательных напряжений, касательные напряжения и в поперечном сечении балки равны:

�=����0���τ=Ix​bQy​Sx0​​​

где

• ��Qy​ — поперечная сила в рассматриваемом сечении балки;

• ��0Sx0​ — статический момент отсеченной части сечения относительно нейтральной оси X;

• ��Ix​ — момент инерции всего сечения относительно нейтральной оси X;

• b — ширина сечения, на уровне точки в которой вычисляется касательное напряжение.

Отсеченная часть — это часть сечения, расположенная выше или ниже точки, где вычисляется касательное напряжение.

Максимальные касательные напряжения при поперечном изгибе появляются в точках, расположенных на нейтральной оси.

Полученная формула называется формулой Журавского и предназначена для вычисления касательных напряжений в произвольной точке сечения при поперечном изгибе балки.

Пример распределения касательных напряжений по высоте сечения балки при ее поперечном изгибе.

Примеры распределения касательных напряжений по высоте сечения