Изгиб бруса, при котором плоскость действия суммарного изгибающего момента в сечении не содержит ни одной из главных осей инерции этого сечения, называется косым изгибом.

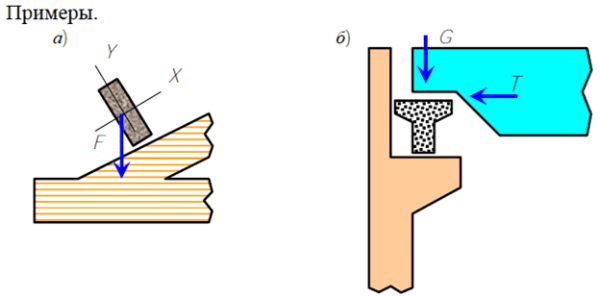
Примеры элементов конструкций, испытывающих косой изгиб: а) обрешетка кровли; б) подкрановая балка

На косой изгиб могут работать обрешетки кровли, подкрановые балки, элементы пространственных стержневых систем и др.

Определение напряжений при косом изгибе

Пусть дана консольная балка прямоугольного сечения, загруженная на конце сосредоточенной силой F.

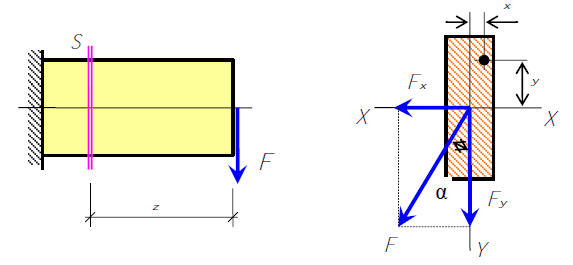
Консольная балка, испытывающая косой изгиб

Разложим силу F на составляющие по направлению оси X и оси Y, являющимися главными осями инерции рассматриваемого сечения в связи с тем, что они являются осями симметрии сечения.

��=�sin⁡�;��=�cos⁡�.Fx​=Fsinα;Fy​=Fcosα.

Каждая из составляющих сил вызывает в сечении S изгибающий момент:

��=��⋅�=�⋅�⋅����=�⋅����;��=��⋅�=�⋅�⋅����=�⋅����;Mx​=Fy​⋅z=F⋅z⋅cosα=M⋅cosα;My​=Fx​⋅z=F⋅z⋅sinα=M⋅sinα;

Таким образом, при косом изгибе в одном сечении действуют два изгибающих момента — момент относительно оси X и момент относительно оси Y. Учитывая принцип независимости действия сил, определим нормальное напряжение в произвольной точке поперечного сечения.

�=�от��+�от��σ=σотMx​​+σотMy​​

или

�=�����+�����σ=Ix​Mx​​y+Iy​My​​x​

• где ��,��Mx​,My​ — изгибающие моменты в сечении относительно главных осей инерции X и Y

• ��,��Ix​,Iy​ — главные центральные моменты инерции рассматриваемого сечения;

• x, y — координаты точки, в которой вычисляется напряжение.

Для получения правильного знака оси X и Y следует направлять в сторону растянутых волокон, изгибающие моменты всегда принимать положительными, а координаты x и y со своим знаком.

����=±����±����⩽�σmax​=±Wx​Mx​​±Wy​My​​⩽R​

• где ��,��Wx​,Wy​ — осевые моменты сопротивления сечения относительно осей X и Y.

  

  Примеры сечений, имеющих точки, максимально удаленные от главных центральных осей инерции – прямоугольное, коробчатое, двутавровое