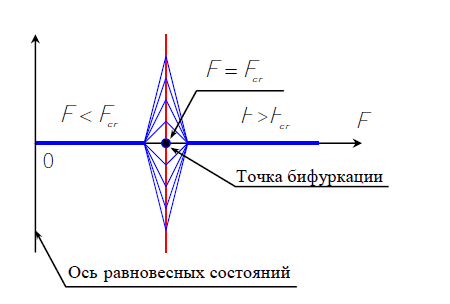
Леона́рд Э́йлер (нем. Leonhard Euler; 4 (15) апреля 1707, Базель, Швейцария — 7 (18) сентября 1783, Санкт-Петербург, Российская империя) — швейцарский, немецкий и российский математик, внёсший значительный вклад в развитие математики, а также механики, физики, астрономии и ряда прикладных наук.

При малой сжимающей силы �<���F<Fcr​ прямолинейный стержень находится в состоянии устойчивого равновесия. Такое состояние только одно — прямолинейная форма (случай 1).

При большой сжимающей силе �>���F>Fcr​ прямолинейный стержень находится в состоянии неустойчивого равновесия. Такое состояние может быть только одно — прямолинейна форма (случай 3).

Но имеется граничное состояние, когда �=���F=Fcr​. В этом случае сжимаемый стержень находится в безразличном состоянии равновесия. Прямолинейная форма равновесия сжатого стержня в этом случае не является единственной. Форм равновесия становится бесконечное множество. При этом и незначительно искривленные стержни тоже будут находиться в состоянии равновесия. То есть происходит бифуркация форм равновесия (случай 2).

Иллюстрация форм равновесия сжатого стержня

Согласно определению Эйлера — наименьшее значение сжимающей силы, при которой происходит разветвление форм равновесия, называется критической силой.

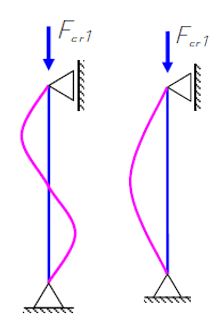
Искривление стержня в форме (в формЕ двух полуволн)одной полуволны

Для реального стержня следует принимать во внимание только минимальную критическую силу.

Формула Эйлера:

���=�2���2Fcr​=i2π2EI​

Формула Эйлера опубликована в 1744 г. Формула Эйлера справедлива только в случае упругой деформации материала стержня, так как при ее выводе используется дифференциальное уравнение упругой оси стержня при изгибе.