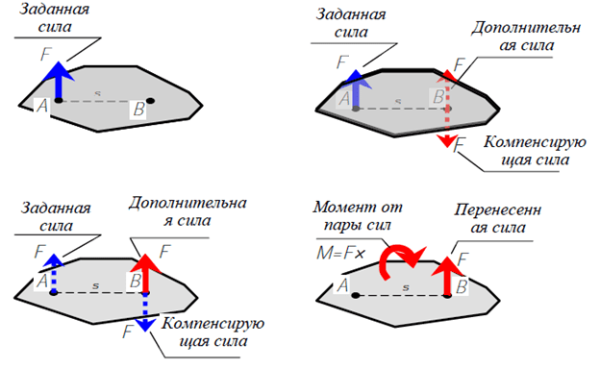
Вначале рассмотрим диск, к которому приложена сила F в точке A. Переместим силу F так, чтобы ее точка приложения оказалась в точке B.

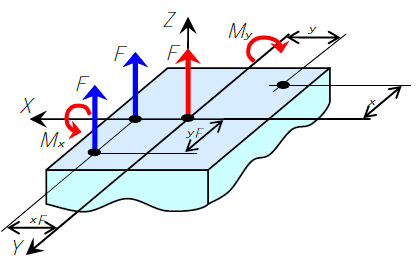
Процесс параллельного перемещения силы

Очевидно, что в результате параллельного переноса силы появляется момент, равный произведению исходной силы на расстояние переноса.

То же самое проделаем и для внецентренно приложенной к колонне силы. Только в этом случае будем перемещать ее дважды. Вначале переместим точку приложения силы на Fy, так, чтобы она оказалась на оси X, а затем на Fx, чтобы она оказалась на продольной оси колонны Z. В результате такого двойного переноса появляются два момента — момент относительно оси X (��=���Mx​=FyF​) и момента относительно оси У (��=���My​=FxF​).

Перенос внецентренно приложенной силы на продольную ось Z

Для удобства рассмотрим внецентренно сжатый стержень прямоугольного поперечного сечения. Это удобно, потому, что заранее известны положения главных центральных осей инерции, которыми будут оси симметрии сечения.

В результате такого переноса кроме центрально приложенной силы F появятся еще два момента Mx и My. Так как эти моменты относительно поперечных осей, то они являются изгибающими.

�=�;��=���;��=���N=F;Mx​=FyF​;My​=FxF​

Таким образом, внецентренное растяжение (сжатие) приводится к трем простым видам сопротивления — центральному растяжению (сжатию) и двум чистым изгибам. Используя принцип независимости действия сил, вычислим напряжения в произвольной точке поперечного сечения стержня от каждого внутренней силы отдельно и сложим их.

�=�от�+�от��+�от��σ=σотN​+σотMx​+σотMy​

или

�=��+�����+�����σ=AN​+Ix​Mx​​y+Iy​My​​x​

Где:

N — продольная сила, равная внецентренно приложенной равнодействующей всех сил, приложенных к колонне �=±�N=±F. Если колонна внецентренно растянута, то принимаем знак «плю», если внецентренно сжата, то принимаем знак «минус».

Mx,My — изгибающие моменты, вызванные эксцентриситетом приложения равнодействующей силы.