Теорема о взаимности работ внешних сил

Эта теорема впервые опубликована итальянским ученым Бетти (1823—1892 гг) и названа его именем.

Рассмотрим два состояния балки.

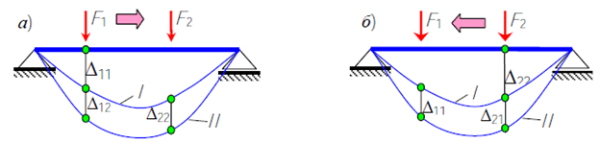
Схема взаимных деформаций балки от действия сил

Поясним обозначения. Первый индекс обозначает направление перемещения, а второй – фактор, вызывающий это перемещение.

• Δ11Δ11​ — перемещение по направлению первой силы от действия первой силы;

• Δ21Δ21​ — перемещение по направлению второй силы от действия первой силы;

• Δ12Δ12​ — перемещение по направлению первой силы от действия второй силы;

• Δ22Δ22​ — перемещение по направлению второй силы от действия второй силы.

Рассмотрим деформации балки при разных последовательностях приложения сил. Первый вариант загружения — вначале прикладываем силу �1F1​, потом силу �2F2​.

Деформации балки от действия первой силы, а затем второй (а) и деформация балки от действия второй силы, а затем первой (б)

Сформулируем теорему о взаимности внешних сил:

Работа внешних сил первого состояния на перемещениях второго состояния равна работе внешних сил второго состояния на перемещениях первого состояния.

�12=�21A12​=A21​