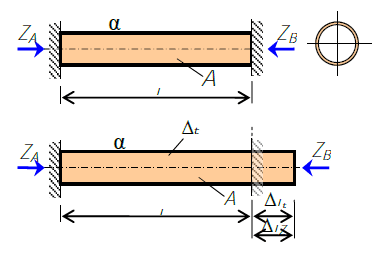
В статически определимых системах изменение температуры вызывает лишь деформации их элементов, так как этому ничто не препятствует. В статически неопределимых системах изменению размеров элементов за счет изменения их температуры препятствуют дополнительные связи. Поэтому изменение температуры статически неопределимой конструкции приводит к появлению температурных напряжений. Температурные напряжения являются опасными и часто приводят к повреждениям или разрушению конструкции.

Рассмотрим стержень кольцевого сечения, подвергнутый температурному воздействию. Пусть температура стержня повысилась на Δt. Большинство материалов при повышении температуры увеличивают свои размеры.

Способность материала деформироваться при изменении температуры характеризуется коэффициентом температурного расширения α, который может быть найден только испытанием и имеет размерность град−1град−1.Значения коэффициента температурного расширения можно найти в справочниках.

Схема стержня, подвергнутого температурному воздействию

Количество уравнений равновесия – 1.

Количество неизвестных реакций – 2.

Степень статической неопределимости n=2-1=1.

Следовательно, система один раз (однажды) статически неопределимая.

Рассмотрим деформации от каждого фактора в отдельности. При повышении температуры стержень удлинится на Δ��Δlt​. От действия реакции ��ZB​ стержень укорачивается наΔ���ΔlZB​.

Уравнение равновесия:

∑�=��−��=0∑Z=ZA​−ZB​=0

Запишем уравнение совместности деформаций:

Δ��+Δ���=ΔΔlt​+ΔlZB​=Δ

По закону Гука и от температуры стержень получит деформации:

Δ���=−��⋅���;Δ��=�⋅�⋅Δ�ΔlZB​=EA−ZB⋅l​;Δlc​=α⋅l⋅Δt

Для стали коэффициент температурного расширения равен α=12,5 град−1ад−1.

Дополнительное уравнение при отсутствии зазора имеет вид:

�⋅�⋅Δ�−��⋅���=0α⋅l⋅Δt−EAZB⋅l​=0

В результате решения системы уравнений получаем значения реакций ��и��ZA​иZB​. Это значит, что статическая неопределимость раскрыта. Дальнейший расчет выполняется как для статически определимого стержня.

Температурные напряжения:

��=−�⋅Δ�⋅�σt​=−α⋅Δt⋅E​

Оказывается, что температурные напряжения не зависят от площади поперечного сечения стержня и его длины. Это следует учитывать при расчете конструкций, подвергнутых температурным воздействиям — увеличение площади поперечных сечений элемента не приводит к уменьшению температурных напряжений. То есть усиление конструкций, испытывающих температурное воздействие, нельзя добиться увеличением площадей поперечных сечений их элементов.

Для снижения температурных напряжений используются специальные приемы проектирования — компенсация температурных напряжений.